Heat Transfer

Transient heat conduction using numerical methods

Lecturer: Jakob Hærvig

Notation for transient problems

  • On space axis $m,n,k$ denote node number in $x,y,z$-directions
    • Distance between nodes is $\Delta x$
  • On time axis $i$ denote node number in $t$-direction (time)
    • Time between nodes is $\Delta t$
  • General notation:

    • $$ T_{m,n,k}^i $$

The energy balance equation for transient problems

We sum up heat transfer to/from volume element:

    $$ \small \left( \begin{array}{ccc} \text{Sum of heat}\\ \text{transfer rate}\\ \text{across surfaces}\\ \text{of volume element} \end{array} \right) + \left( \begin{array}{ccc} \text{Rate of heat}\\ \text{generation}\\ \text{inside the}\\ \text{element} \end{array} \right) = \left( \begin{array}{ccc} \text{Rate of change}\\ \text{of the energy}\\ \text{content of}\\ \text{the element} \end{array} \right) $$

  • For transient heat transfer (temperature changes with time):

    $$ \small \sum_\text{all surfaces} \dot{Q} + \dot{G}_\text{element} = \frac{\Delta E_\text{element}}{\Delta t} $$

    $$ \small \sum_\text{all surfaces} \dot{Q} + \dot{G}_\text{element} = m c_p \frac{\Delta T_\text{element}}{\Delta t} $$

    $$ \small \sum_\text{all surfaces} \dot{Q} + \dot{G}_\text{element} = V_\text{element} \rho c_p \frac{\Delta T_\text{element}}{\Delta t} $$

    • Explicit and implicit solution methods

    Question is: How do we advance from time $t$ (timestep $i$) to timestep $t+\Delta t$ (timestep $i+1$)?

    Explicit method

    \(\displaystyle \sum_\text{all surfaces} \textcolor{#008000}{Q^i} + \textcolor{#008000}{\dot{G}_\text{element}^i} \) \(\displaystyle =\) \(\displaystyle \frac{\rho V_\text{element} c_p (T_m^{i+1}-T_m^i)}{\Delta t} \)

    Implicit method

    \(\displaystyle \sum_\text{all surfaces} Q^{i+1} + \dot{G}_\text{element}^{i+1} \) \(\displaystyle =\) \(\displaystyle \frac{\rho V_\text{element} c_p (T_m^{i+1}-T_m^i)}{\Delta t} \)

    Explicit: Use data from current time step $i$ (all known temperatures)

    Implicit: Use data from next time step $i+1$ (unknown temperatures)

    Transient heat conduction using the explicit method

    Interior nodes using explicit solution method

    Energy balance at interior node:

      $$\begin{aligned} kA\frac{\textcolor{#008000}{T_{m-1}^i}-\textcolor{#008000}{T_{m}^i}}{\Delta x} + kA\frac{\textcolor{#008000}{T_{m+1}^i}-\textcolor{#008000}{T_{m}^i}}{\Delta x}+ \dot{g}_\text{m}^iA\Delta x=\frac{\rho V c_p (T_m^{i+1}-T_m^i)}{\Delta t} \end{aligned}$$
    • Re-arranging and inserting thermal diffusivity $\alpha=k/(\rho c_p)$:
      • $$\begin{aligned} \textcolor{#008000}{T_{m-1}^i}-2\textcolor{#008000}{T_{m}^i}+\textcolor{#008000}{T_{m+1}^i} + \frac{\dot{g}_m^i \Delta x^2}{k} = \frac{\Delta x^2}{\alpha \Delta t}\left(T_m^{i+1}-T_m^i\right) \end{aligned}$$
    • Inserting mesh Fourier number $\tau=\alpha\Delta t/\Delta x^2$:
      • $$\begin{aligned} \textcolor{#008000}{T_{m-1}^i}-2\textcolor{#008000}{T_{m}^i}+\textcolor{#008000}{T_{m+1}^i} + \frac{\dot{g}_m^i \Delta x^2}{k} = \frac{1}{\tau}\left(T_m^{i+1}-T_m^i\right) \end{aligned}$$
    • Isolating the only unknown $\textcolor{#b52025}{T_m^{i+1}}$:
      • $$\begin{aligned} \textcolor{#b52025}{T_m^{i+1}} = \tau(T_{m-1}^i+T_{m+1}^i)+(1-2\tau)T_m^i+\tau\frac{\dot{g}_m^i \Delta x^2}{k} \end{aligned}$$
    • 1 equation for each node with only 1 unknown each 😎

    Boundary nodes using explicit solution method

    Energy balance for boundary node with convection:

      $$\begin{aligned} hA(T_\infty-\textcolor{#008000}{T_0^i}) + kA\frac{\textcolor{#008000}{T_1^i}-\textcolor{#008000}{T_0^i}}{\Delta x}+ \dot{g}_\text{0}^iA\frac{\Delta x}{2}=\frac{\rho V c_p (T_0^{i+1}-T_0^i)}{\Delta t} \end{aligned}$$
    • Re-arranging and noting thermal diffusivity $\alpha=k/(\rho c_p)$:
      • $$\begin{aligned} \left(\frac{-2h\Delta x}{k}-2\right)\textcolor{#008000}{T_0^i}+2\textcolor{#008000}{T_{1}^i}+\left(\frac{-2h\Delta x}{k}\right)T_\infty+\dot{g}_0^i\frac{(\Delta x)^2}{k} = \frac{(\Delta x)^2}{\alpha \Delta t}\left(T_0^{i+1}-T_0^i\right) \end{aligned}$$
    • Defining mesh Fourier number $\tau=\alpha\Delta t/\Delta x^2$:
      • $$\begin{aligned} \left(\frac{-2h\Delta x}{k}-2\right)\textcolor{#008000}{T_0^i}+2\textcolor{#008000}{T_{1}^i}+\left(\frac{-2h\Delta x}{k}\right)T_\infty+\dot{g}_0^i\frac{(\Delta x)^2}{k} = \frac{1}{\tau}\left(T_0^{i+1}-T_0^i\right) \end{aligned}$$
    • Isolating the only unknown $\textcolor{#b52025}{T_m^{i+1}}$:
      • $$\begin{aligned} \textcolor{#b52025}{T_0^{i+1}} = \left(1-2\tau-2\tau \frac{h \Delta x}{k}\right)\textcolor{#008000}{T_0^i}+(2\tau)\textcolor{#008000}{T_1^i}+2\tau\frac{h\Delta x}{k}T_\infty+\frac{\tau\dot{g}_0^i(\Delta x)^2}{k} \end{aligned}$$
    • 1 equation for each boundary node with only 1 unknown 😎

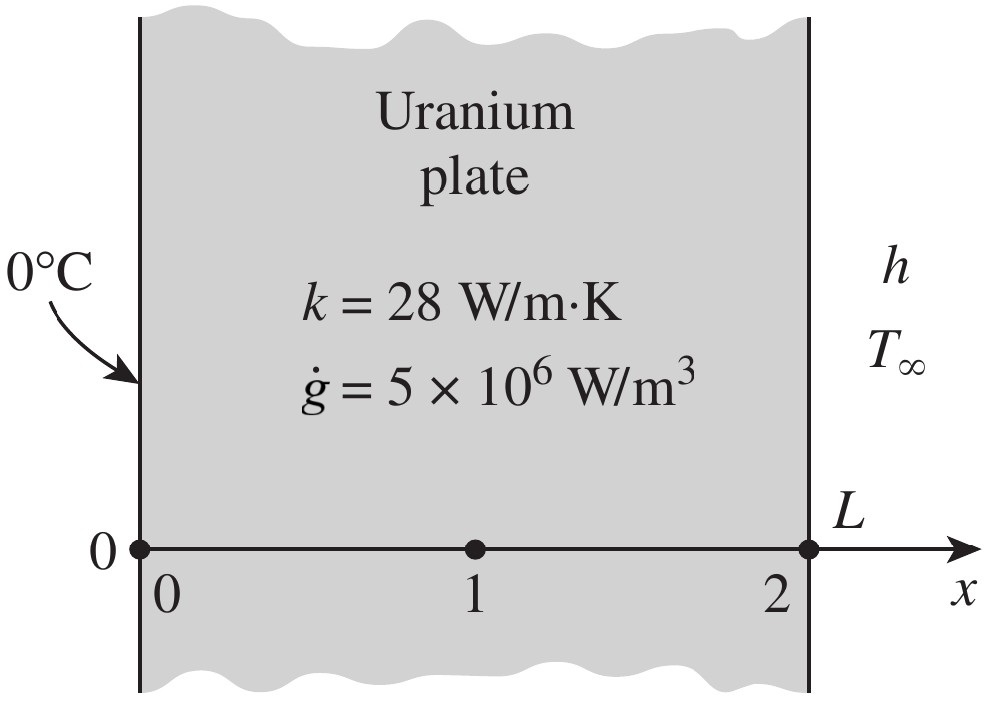
    Example: Transient heat conduction in a large plate using the explicit method

    Consider a large uranium plate of thickness $L=4$ cm, thermal conductivity $k=28$ W/(m·K), and thermal diffusivity
    $a=12.5 \times 10^{-6}$ m$^2$/s that is initially at a uniform temperature of 200°C. Heat is generated uniformly in the plate at a constant rate of
    $\dot{g}=5 \times 10^6$ W/m$^3$.
    At time $t = 0$ s, one side of the plate is brought into contact with iced water and is maintained at 0°C at all times, while the other side is subjected to convection to an environment at $T_\infty=30$°C with a heat transfer coefficient of $h=45$ W/(m$^2$·K).

    Estimate the exposed surface temperature of the plate 2.5 min after start of cooling. Use three equally spaced nodes in the medium, two at the boundaries and one at the middle.

    The stability criterion for the explicit solution method

    Observation: Explicit solution method may diverge if time step size is too large!

    Stability criterion: When looking at node $m$, the coefficient in front of $T_m^i$ should be larger than zero

  • Equation for an interior node (derived here):

    \( \displaystyle T_m^{i+1} = \tau(T_{m-1}^i+T_{m+1}^i) \) \(+ \) \( \displaystyle (1-2\tau) \) \( \displaystyle T_m^i+\tau\frac{\dot{g}_m^i (\Delta x)^2}{k}\)

    • Criterion becomes: $ \displaystyle 1-2\tau \geq 0$ $\quad \rightarrow \quad$ $\displaystyle 1-2(\alpha \Delta t/ \Delta x^2)\geq0$ $\quad \rightarrow \quad$ $\displaystyle \Delta t \leq \frac{(\Delta x)^2}{2\alpha}$

  • Equation for a boundary node with convection (derived here):

    \( \displaystyle T_0^{i+1} \) \( \displaystyle = \) \( \displaystyle \left(1-2\tau-2\tau \frac{h \Delta x}{k}\right) \) \( \displaystyle T_0^i + \) \( \displaystyle (2\tau) \) \( \displaystyle T_1^i \) \( \displaystyle + 2\tau\frac{h\Delta x}{k}T_\infty+\frac{\tau\dot{g}_0^i(\Delta x)^2}{k} \)

    • Criterion becomes: $ \displaystyle\left(1-2\tau-2\tau \frac{h \Delta x}{k}\right)\geq 0$ $\quad \rightarrow \quad$ $\displaystyle \Delta t \leq \frac{(\Delta x)^2}{2\alpha(1+ \frac{h \Delta x}{k})}$

    • Transient heat conduction using the implicit method

    Interior nodes using implicit solution method

    Energy balance at interior node:

      $$\begin{aligned} kA\frac{\textcolor{#524fa1}{T_{m-1}^{i+1}}-\textcolor{#524fa1}{T_{m}^{i+1}}}{\Delta x} + kA\frac{\textcolor{#524fa1}{T_{m+1}^{i+1}}-\textcolor{#524fa1}{T_{m}^{i+1}}}{\Delta x}+ \dot{g}_\text{m}^{i+1}A\Delta x=\frac{\rho V c_p (T_m^{i+1}-T_m^i)}{\Delta t} \end{aligned}$$
    • Re-arranging:
      • $$\begin{aligned} \textcolor{#524fa1}{T_{m-1}^{i+1}}-2\textcolor{#524fa1}{T_{m}^{i+1}}+\textcolor{#524fa1}{T_{m+1}^{i+1}} + \frac{\dot{q}_m^{i+1} \Delta x^2}{k} = \frac{\Delta x^2}{\alpha \Delta t}\left(T_m^{i+1}-T_m^i\right) \end{aligned}$$
    • Using $\tau=\alpha\Delta t/\Delta x^2$:
      • $$\begin{aligned} \textcolor{#524fa1}{T_{m-1}^{i+1}}-2\textcolor{#524fa1}{T_{m}^{i+1}}+\textcolor{#524fa1}{T_{m+1}^{i+1}} + \frac{\dot{q}_m^{i+1} \Delta x^2}{k} = \frac{1}{\tau}\left(T_m^{i+1}-T_m^i\right) \end{aligned}$$
    • Seperating the 3 unknowns $\textcolor{#b52025}{T_{m-1}^{i+1}}$, $\textcolor{#b52025}{T_m^{i+1}}$ and $\textcolor{#b52025}{T_{m+1}^{i+1}}$:
      • $$\begin{aligned} \tau\textcolor{#b52025}{T_{m-1}^{i+1}} - (1+2\tau) \textcolor{#b52025}{T_m^{i+1}} + \tau \textcolor{#b52025}{T_{m+1}^{i+1}} + \tau \frac{\dot{g}_m^{i+1}\Delta x^2}{k} + T_m^i = 0 \end{aligned}$$
    • Can't solve each equation individually because each equation has three unknowns, $T_{m-1}^{i+1}$, $T_m^{i+1}$, and $T_{m+1}^{i+1}$ 😒

    Boundary nodes using implicit solution method

    Energy balance at boundary node with convection:

      $$\begin{aligned} hA(T_\infty-\textcolor{#524fa1}{T_0^{i+1}}) + kA\frac{\textcolor{#524fa1}{T_1^{i+1}}-\textcolor{#524fa1}{T_0^{i+1}}}{\Delta x}+ \dot{g}_\text{m}^{i+1}A\frac{\Delta x}{2}=\frac{\rho V c_p (T_0^{i+1}-T_0^i)}{\Delta t} \end{aligned}$$
    • Re-arranging:
      • $$\begin{aligned} \left(\frac{-2h\Delta x}{k}-2\right)\textcolor{#524fa1}{T_0^{i+1}}+2\textcolor{#524fa1}{T_{1}^{i+1}}+\left(\frac{2h\Delta x}{k}\right)T_\infty+\dot{g}_0^i\frac{(\Delta x)^2}{k} = \frac{(\Delta x)^2}{\alpha \Delta t}\left(T_0^{i+1}-T_0^i\right) \end{aligned}$$
    • Defining $\tau=\alpha\Delta t/\Delta x^2$:
      • $$\begin{aligned} \left(\frac{-2h\Delta x}{k}-2\right)\textcolor{#524fa1}{T_0^{i+1}}+2\textcolor{#524fa1}{T_{1}^{i+1}}+\left(\frac{2h\Delta x}{k}\right)T_\infty+\dot{g}_0^i\frac{(\Delta x)^2}{k} = \frac{1}{\tau}\left(T_0^{i+1}-T_0^i\right) \end{aligned}$$
    • Seperating the 2 unknowns $\textcolor{#b52025}{T_0^{i+1}}$ and $\textcolor{#b52025}{T_1^{i+1}}$:
      • $$\begin{aligned} \left(-1-2\tau-2\tau \frac{h \Delta x}{k}\right)\textcolor{#b52025}{T_0^{i+1}}+(2\tau)\textcolor{#b52025}{T_1^{i+1}}+2\tau\frac{h\Delta x}{k}T_\infty+\tau \frac{\dot{g}_0^{i+1}(\Delta x)^2}{k}+T_0^i=0 \end{aligned}$$
    • Can't solve each equation individually because each equation has two unknowns, $T_0^{i+1}$ and $T_1^{i+1}$ 😒

    Example: Transient heat conduction in a large plate using the implicit method

    Consider a large uranium plate of thickness $L=4$ cm, thermal conductivity $k=28$ W/(m·K), and thermal diffusivity
    $a=12.5 \times 10^{-6}$ m$^2$/s that is initially at a uniform temperature of 200°C. Heat is generated uniformly in the plate at a constant rate of
    $\dot{g}=5 \times 10^6$ W/m$^3$.
    At time $t = 0$ s, one side of the plate is brought into contact with iced water and is maintained at 0°C at all times, while the other side is subjected to convection to an environment at $T_\infty=30$°C with a heat transfer coefficient of $h=45$ W/(m$^2$·K).

    Estimate the exposed surface temperature of the plate 2.5 min after start of cooling. Use three equally spaced nodes in the medium, two at the boundaries and one at the middle.