Heat Transfer
Lumped system assumption
Lecturer: Jakob Hærvig
What is the lumped system assumption and why?
Most heat transfer problems are complex because temperature varies with both space and time
\(\quad T=f(x,y,z,t)\) \(\quad \rightarrow \quad\) \(\quad T=f(t)\)
Starting point of lumped system analysis
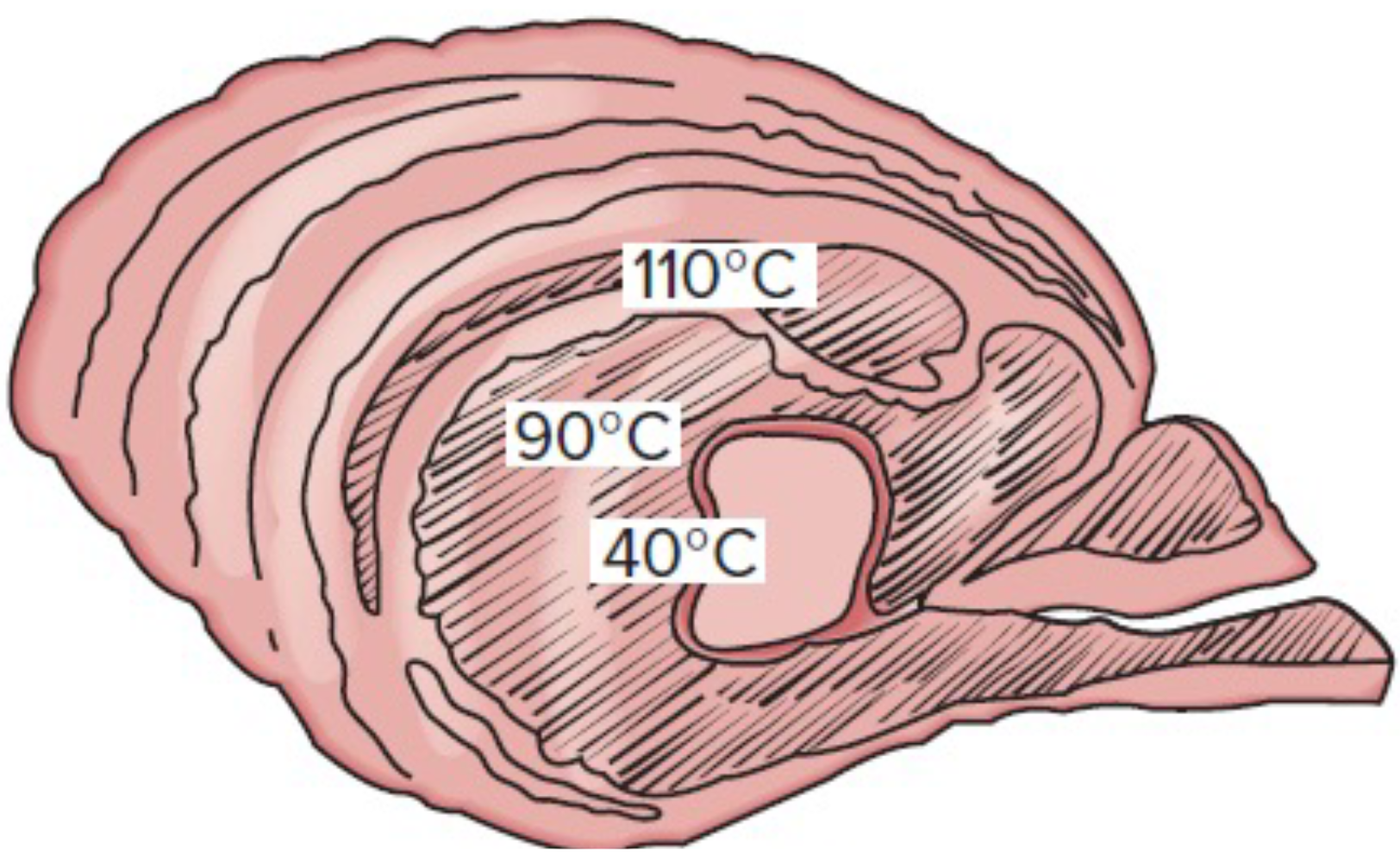
Consider a body of arbitrary shape with
- At time $t=0$ the body is exposed to convective heat transfer from the outside:
- Surrounding temperature $T_\infty$
- Heat transfer coefficient $h$
- Surface area $A_s$
Derivation of the lumped system equation
Energy transferred to body during $\text{d}t$:
\(\dot{Q}=h A_s (T_\infty-T) \text{d}t \) \(= m c_p \text{d}T\) \( =\rho V c_p \text{d}T\)
Because $T_\infty$ is constant, we may expand $\text{d}T$:
\(\dot{Q}=h A_s (T_\infty-T) \text{d}t = \rho V c_p \text{d}(T-T_\infty)\)
..Re-arranging:
$$ \frac{\text{d}(T-T_\infty)}{T-T_\infty} = -\frac{h A_s}{\rho V c_p} \text{d}t$$
Now, intergrate from $t=0$ where $T=T_i$ to $t$ at which $T=T(t)$:
\( \displaystyle\text{ln}\frac{T(t)-T_\infty}{T_i-T_\infty} = -\frac{h A_s}{\rho V c_p}t\)
Exponential on both sides gives lumped system equation:
\( \displaystyle \frac{T(t)-T_\infty}{T_i-T_\infty} = \text{e}^{-\frac{h A_s}{\rho V c_p}t}\)
The time constant for lumped systems
Introducing $b=hA_s/(\rho V c_p)$, we obtain:
\( \displaystyle \frac{T(t)-T_\infty}{T_i-T_\infty} = \text{e}^{-\frac{h A_s}{\rho V c_p}t} = \text{e}^{-bt}\)
The time constant ($1/b$) describes the rate at which the system approaches the surrounding temperature $T_\infty$
- Large $b$: Temperature approaches $T_\infty$ quickly
- Small $b$: Temperature approaches $T_\infty$ slowly
Validity of lumped system assumption
We define a Biot number
- with the characteristic length $L_c=V/A_s$
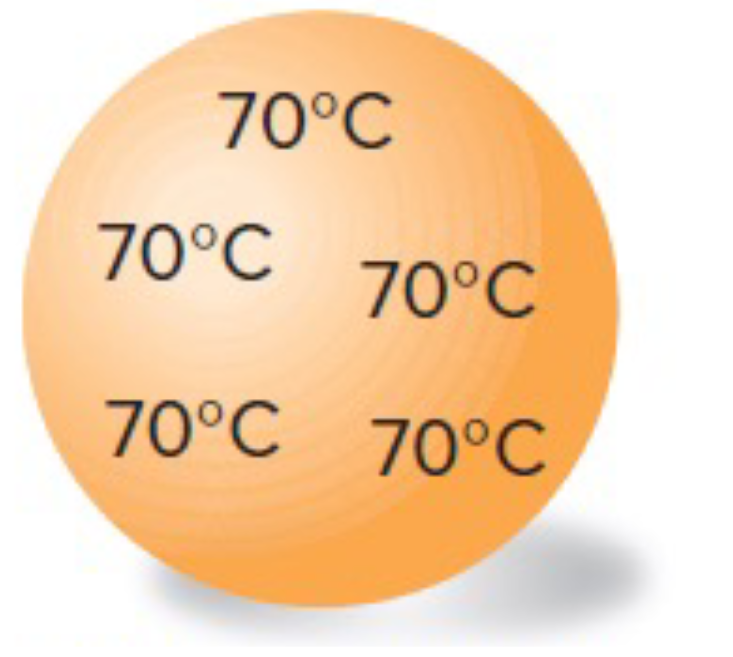
If $\text{Bi}=0$: lumped system assumption is exact
If $\text{Bi}\leq 0.1$: lumped system assumption is resonable accurate
If $\text{Bi}> 0.1$: lumped system assumption is inaccurate
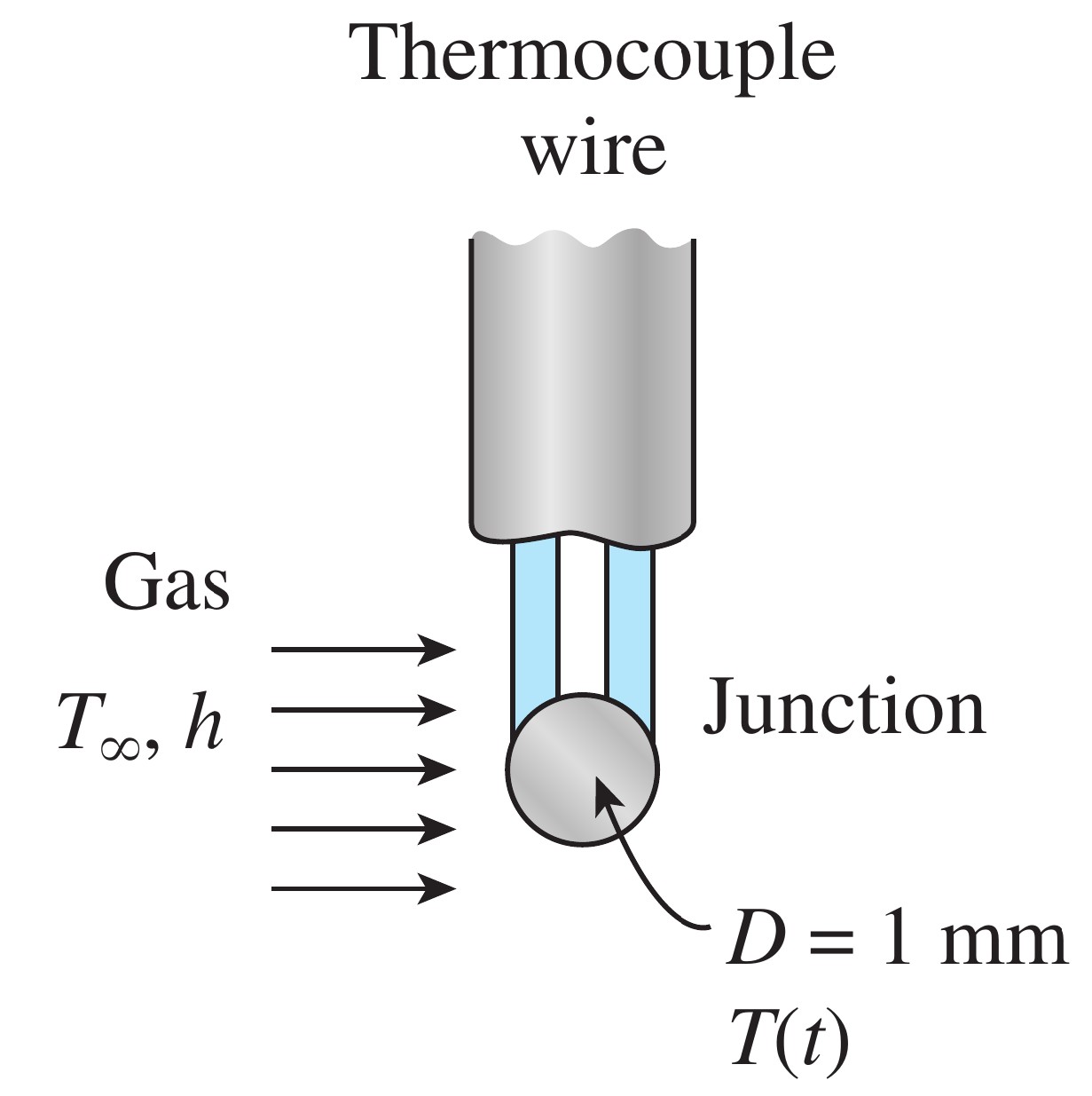
Example: Fast temperature measurements with thermocouples
The temperature of a gas stream is to be measured by a thermocouple. The thermocouple junction can be
approximated as a 1 mm diameter sphere.
The junction properties are $k=35$ W/m·K, $\rho=8500$ kg/m$^3$ and $c_p=320$ J/kg·K.
How quickly can
the thermocouple respond to changes in temperature when the convective heat transfer coefficient between
the junction and the gas is $h=210$ W/m$^2$·K?