Fluid Mechanics

Dimensional analysis

Lecturer: Jakob Hærvig

Slides by Jakob Hærvig (AAU Energy) and Jacob Andersen (AAU Build)

Why look at dimensional analysis?

The basis for all dimensional analysis

Total of seven base dimensions in the MLT system:

  1. Mass, $\text{M}$
  2. Length, $\text{L}$
  3. Time, $\text{T}$
  4. Temperature, θ
  5. Amount of substance, $\text{N}$
  6. Electrical current, $\text{I}$
  7. Luminous intensity, $\text{C}$

All derived dimensions can be expressed in terms of these base dimensions:

  • Velocity, [$V$] = $\text{LT}^{-1}$
  • Acceleration, [$a$] = $\text{LT}^{-2}$
  • Force, [$F$] = $\text{MLT}^{-2}$
  • Energy, [$E$] = $\text{ML}^{2}\text{T}^{-2}$
  • ...

.. we may also use the FLT system:

  1. Force, $\text{F}$
  2. Length, $\text{L}$
  3. Time, $\text{T}$
  4. ...

Simply convert between $\text{MLT}$ and $\text{FLT}$ by $\text{F}=\text{MLT}^{-2}$.

MLT systems in the wild..

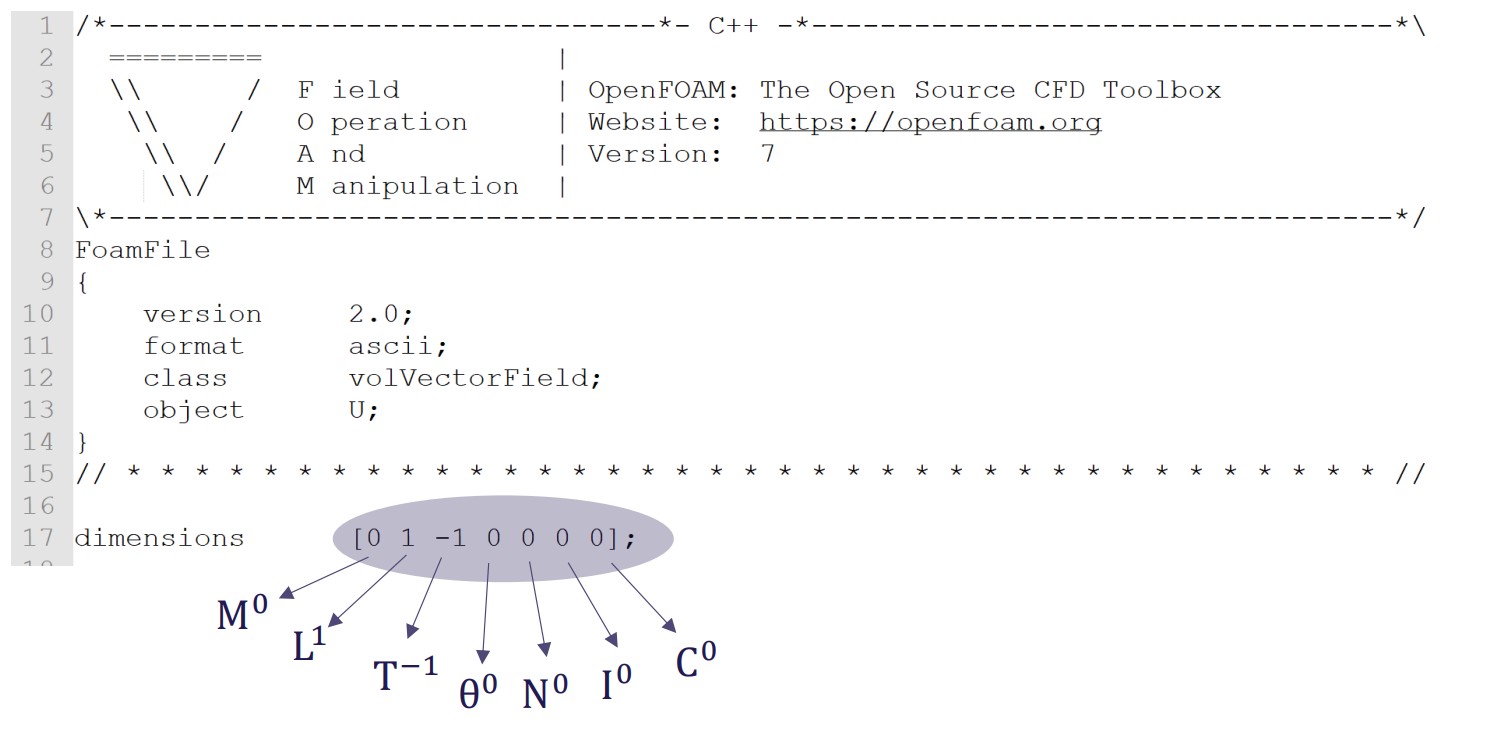
Dimensions in OpenFOAM are defined in terms of the MLT system (here velocity)

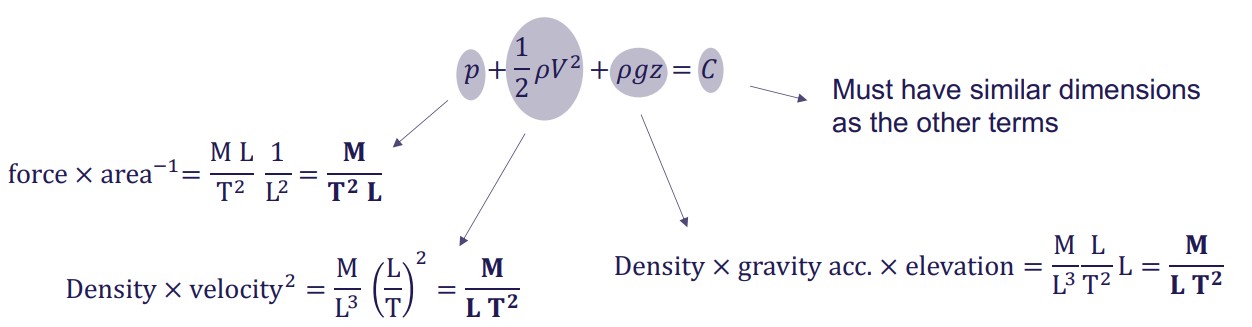
Law of Dimensional Homogeneity

Every additive term ($+$ or $-$) in an equation must have same dimensions

Class exercise 1: Dimensional homogeneity

If $V$ is a velocity, determine the dimensions of $Z$, $\alpha$ and $G$, which appear in the dimensionally homogeneous equation

\( V=Z(\alpha-1)+G \)

Solution without dimensional analysis (don't try this at home)

Problem: Investigate pressure drop drop per unit length pipe $\Delta p_l$

  • Variables expected to be important: Velocity $V$, diameter $D$, dynamic viscosity $\mu$, density $\rho$, length $L$
  • Thus, we may write: $\Delta p = f(V, D, \mu, \rho)$

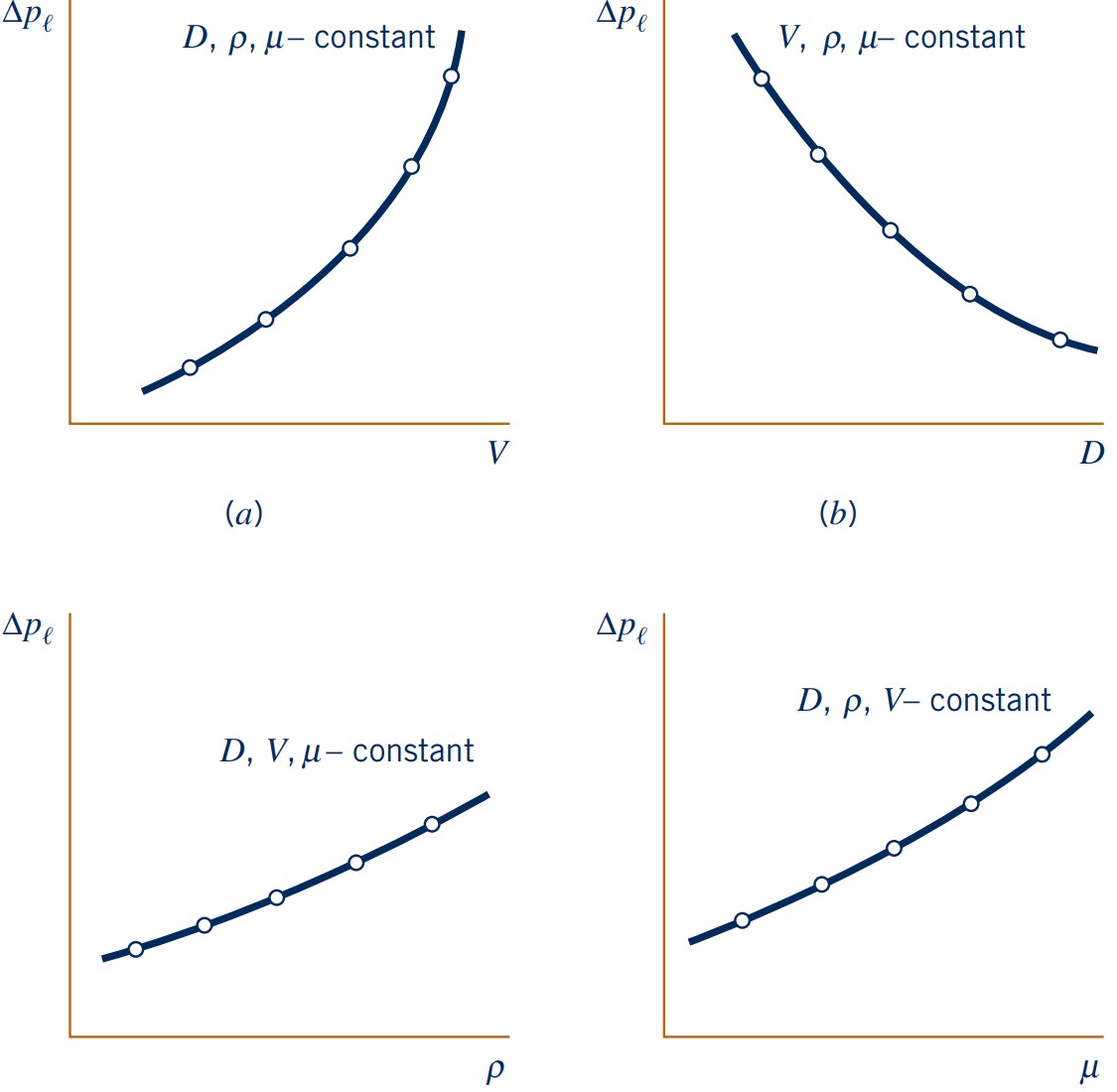
Very tedious approach: Vary one parameter at a time while keeping others constant

  • Requires a lot of experiments/simulations
  • Experiments will be very costly and time-consuming (vary viscosity or density - good luck!)
  • Results are only valid for the specific parameters chosen
  • Difficult to generalise results to other situations
  • Full parameter span (4 parameters with 5 variations)
    requires $5^4=625$ experiments/simulations

Solution with dimensional analysis

Problem: Investigate pressure drop per unit length pipe $\Delta p_l$

  • Variables expected to be important: Velocity $V$, diameter $D$, dynamic viscosity $\mu$, density $\rho$, length $L$
  • Thus, we may write: $\Delta p = f(V, D, \mu, \rho)$
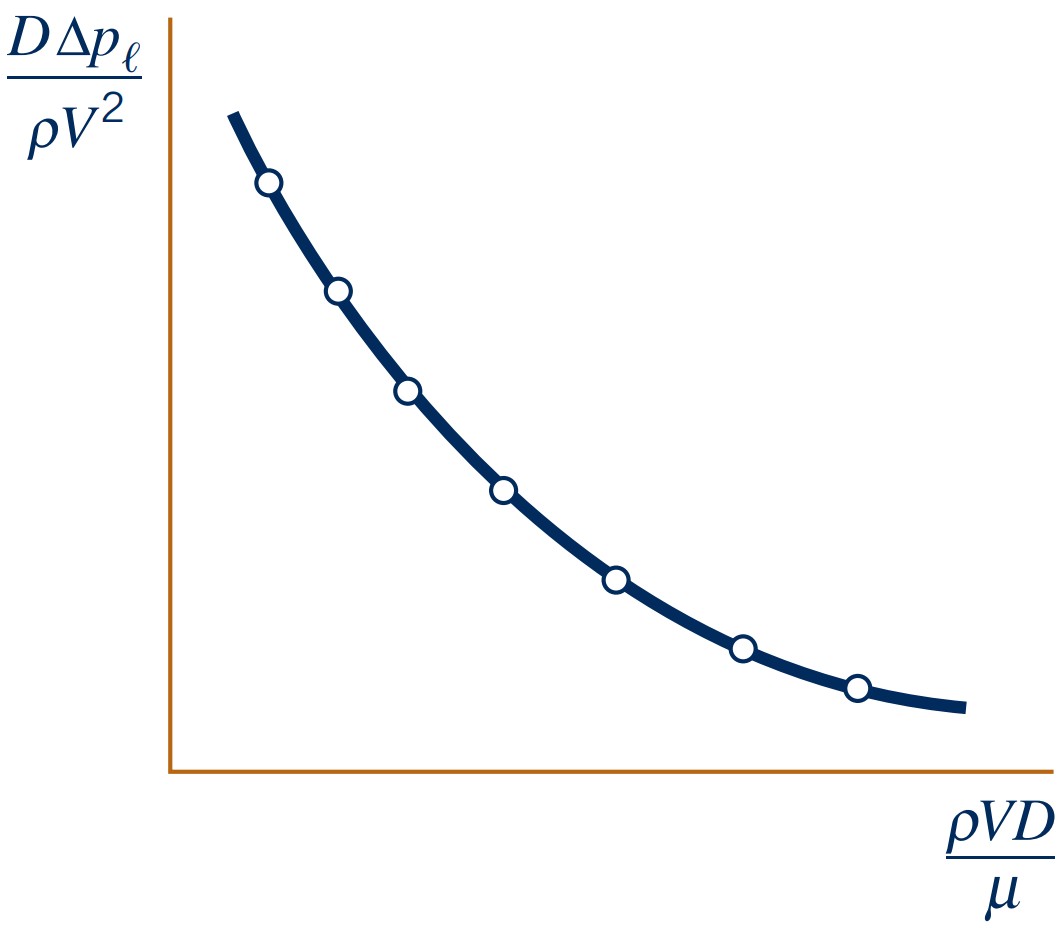
  • Now, transform to dimensionless form: \[\dfrac{D \Delta p}{\rho V^2} = f\left(\dfrac{\rho V D}{\mu}\right)\]

Problem now much simpler: Only need to vary one parameter!

  • Universal solution found (results valid for all pipe flows!)
  • Not costly (few experiments needed)

Buckingham Pi Theorem

Theorem: If an equation (read problem) involves $k$ variables and is dimensionally homogeneous, it can be re-expressed in terms of a set
$k - r$ dimensionless numbers $\Pi_1, \Pi_2, ..., \Pi_{k-r}$, where $r$ is the minimum number of base dimensions required to describe the variables involved.

  1. Identify number of variables, $k$, involved in the problem:

    2. \( x_1 = f(x_2, x_3, \ldots, x_k) \)

  2. Count number of base dimensions, $r$, involved in the problem

  3. Determine the number of required non-dimensional groups, $k-r$ (Buckingham Pi Theorem)

    4. \( \Pi_1 = f(\Pi_2, \Pi_3, \ldots, \Pi_{k-r}) \)

Class exercise 2: Use Buckingham Pi Theorem to determine number of non-dimensional groups

Determine the number of non-dimensional groups required to describe pressure loss per unit length pipe for laminar flow using Buckingham Pi Theorem:


  1. Identify number of variables, $k$, involved in the problem:
  2. Count number of base dimensions, $r$, involved in the problem
  3. Determine the number of required non-dimensional groups, $k-r$ (Buckingham Pi Theorem)

Method of Repeating Variables

Method of Repeating Variables provides a systematic way of constructing the non-dimensional groups for a problem

  1. Identify number of variables, $k$, involved in the problem
  2. Count number of base dimensions, $r$, involved in the problem
  3. Determine the number of required non-dimensional groups, $k-r$ (Buckingham Pi Theorem)
  4. Select a number of repeating variables, where the number of repeating variables equals the number of base dimensions $r$
  5. Construct a non-dimensional group by multiplying one of the non-repeating variables by the product of the repeating variables, each raised to an exponent that will make the group dimensionless
  6. Repeat step 5 for each of the remaining non-repeating variables
  7. Check if the numbers formed are actually non-dimensional
  8. Re-arrange the numbers to more common groups (if such exist)
  9. Relax and think about the results

Class exercise 3: Use method of repeating variables to form non-dimensional groups

Determine the non-dimensional groups required to describe pressure loss per unit length pipe for laminar flow
using the method of repeating variables

  1. Identify number of variables, $k$, involved in the problem
  2. Count number of base dimensions, $r$, involved in the problem
  3. Determine the number of required non-dimensional groups, $k-r$ (Buckingham Pi Theorem)
  4. Select a number of repeating variables, where the number of repeating variables equals the number of base dimensions $r$
  5. Construct a non-dimensional group by multiplying one of the non-repeating variables by the product of the repeating variables, each raised to an exponent that will make the group dimensionless
  6. Repeat step 5 for each of the remaining non-repeating variables
  7. Check if the numbers formed are actually non-dimensional
  8. Re-arrange the numbers to more common groups (if such exist)
  9. Relax and think about the results

Additional comments for

Step 1: Identify number of variables, $k$, involved in the problem

  • What if we pick too few variables?
    • .. forgot surface roughness for turbulent flow:
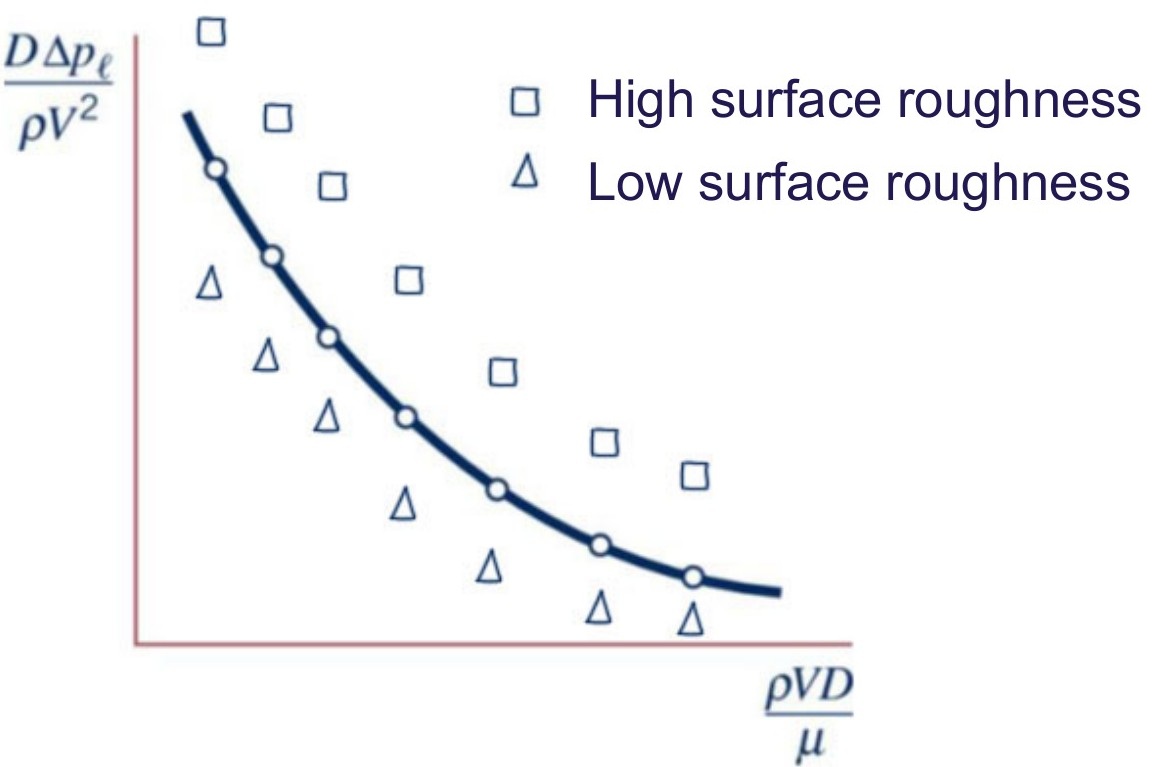
  • Conclusion: Data does not collapse to one line

  • What if we pick too many variables?
    • .. include surface roughness for laminar flow:
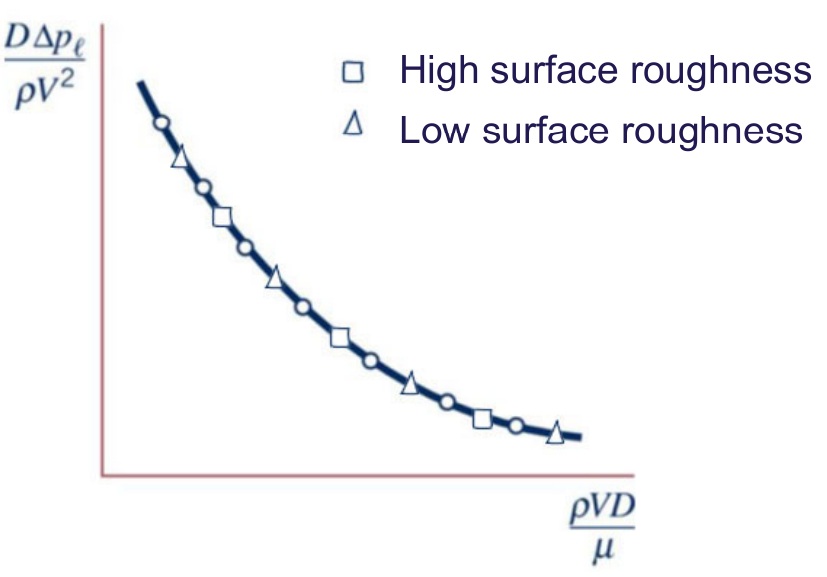
  • Conclusion: All data on one line

Additional comments for

Step 2: Count number of base dimensions, $r$, involved in the problem

  • Does it matter if we use $\text{M}\text{L}\text{T}$ or use $\text{F}\text{L}\text{T}$ system?
    • .. take a look at the following:

    Variable MLT FLT
    Deflection, $\delta$ L L
    Diameter, $D$ L L
    Height, $h$ L L
    Thickness, $d$ L L
    Specific gravity, $\gamma$ $\text{M}\text{L}^{-2}\text{T}^{-2}$ $\text{F}\text{L}^{-3}$
    Young's modulus, $E$ $\text{M}\text{L}^{-1}\text{T}^{-2}$ $\text{F}\text{L}^{-1}$

    • $\text{FLT}$: 2 base dimensions ($\text{F}$ and $\text{L}$)
    • $\text{MLT}$: 2 base dimensions ($\text{M}\text{T}^{-2}$ and $\text{L}$)

  • Conclusion: No, but we should be careful..

Additional comments for

Step 4: Select a number of repeating variables, where the number of repeating variables equals the number of base dimensions $r$

  • Does it matter which ones we choose?
  • Conclusion: No, but..

    • Pick variables that together represent all the base dimensions involved in the problem

    • Don't pick the dependent variable as a repeating variable (the one we interested in)
      • .. otherwise it will appear in more non-dimensional groups

    • Don't pick variables that are already dimensionless (angles, for example)

    • Don't pick variables that can form a dimensionless group by themselves
      • .. such as diameter $[D]=\text{L}$ and height $[H]=\text{L}$

    • Don't pick variables with the same dimensions, or vary by an exponent (e.g. $\text{LT}^{-1}$ and $\text{L}^2\text{T}^{-2}$)

    • Pick variables that are easy to measure or control
      • .. it's easier to vary velocity than viscosity later on..

Additional comments for

Step 4: Select a number of repeating variables, where the number of repeating variables equals the number of base dimensions $r$

  • Functions depend on choice of repeating variables
  • Conclusion: End result is the same in terms of $\Delta p_l$ but functions are different

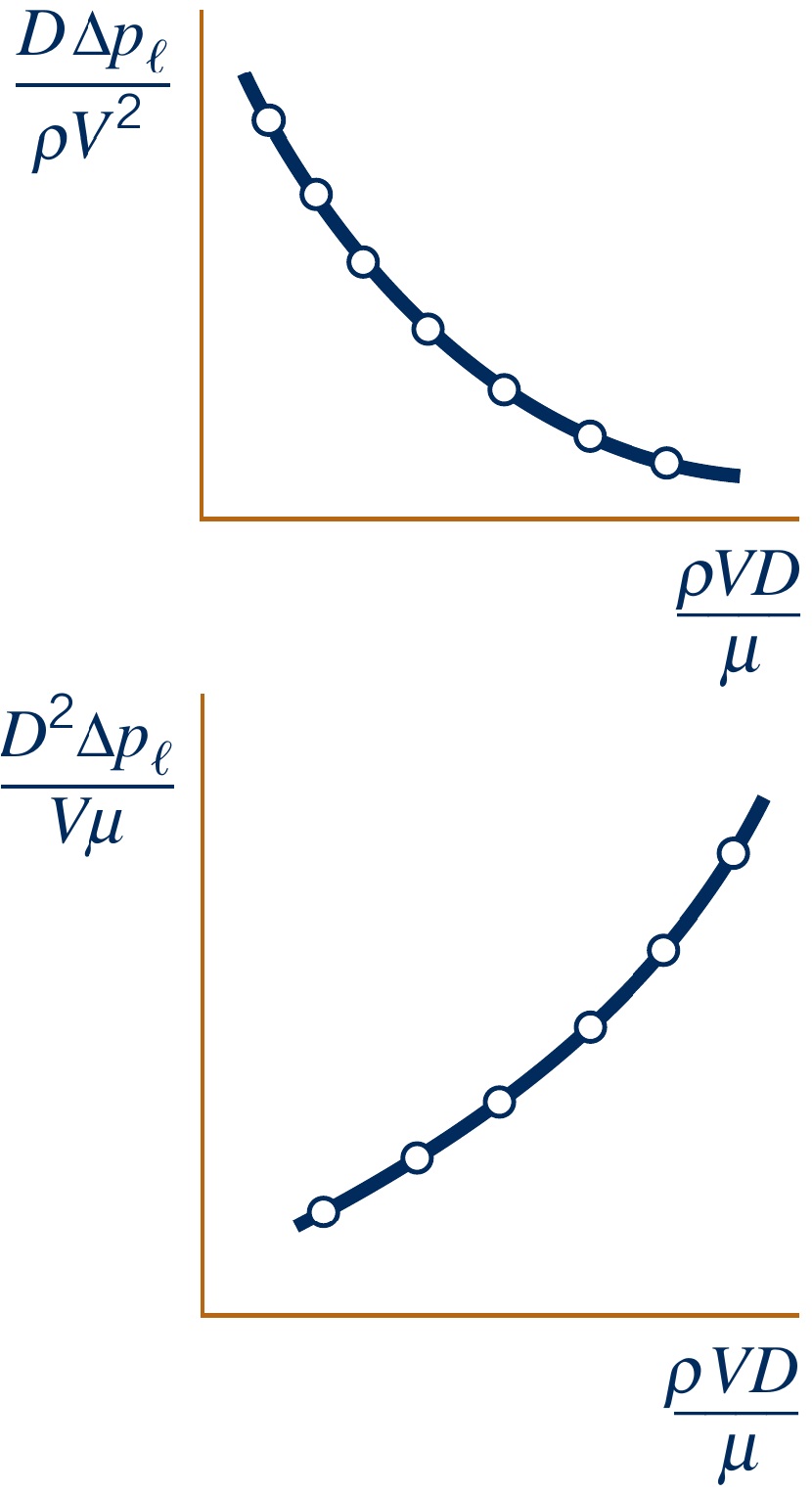
Forming non-Dimensional groups by simple inspection

An alternative to the systematic method of repeating variables

  1. Identify number of variables, $k$, involved in the problem
  2. Count number of base dimensions, $r$, involved in the problem
  3. Determine the number of required non-dimensional groups, $k-r$ (Buckingham Pi Theorem)
  4. Form the non-dimensional groups by inspection, ensuring each group is dimensionless

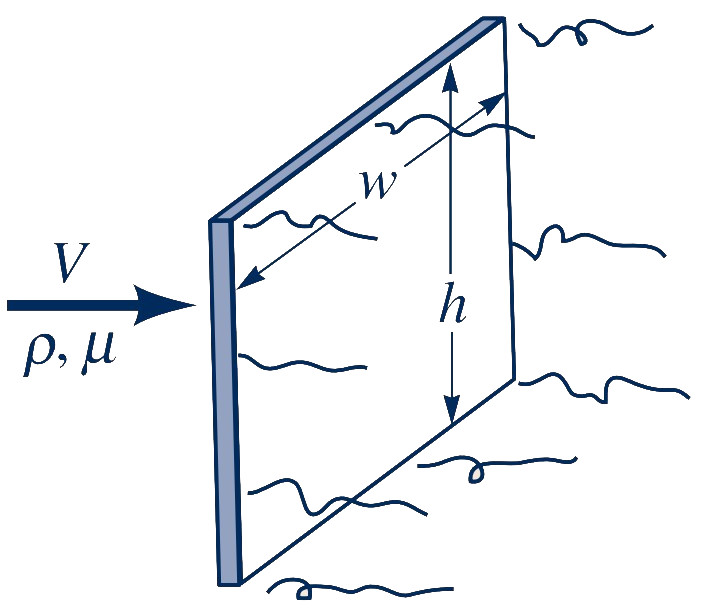
Class exercise 4: Use simple inspection to form non-dimensional groups

Determine by inspection the non-dimensional groups required to describe drag $F_D$ on a flat plate.

Dimensionless numbers are important for dimensional analysis

Similitude

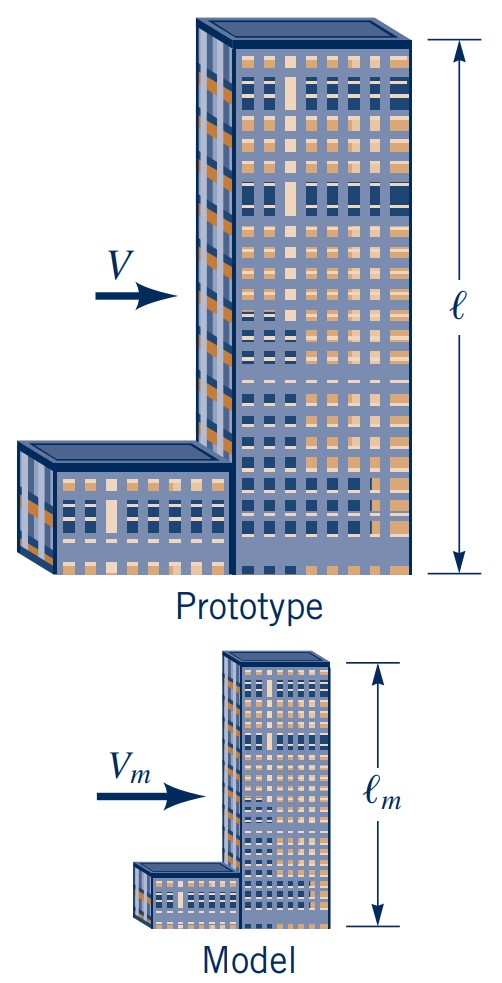
  • A prototype refers to the real thing (e.g. full-scale aircraft, building, bridge, etc.)
  • A model refers to a smaller (or sometimes larger) representation of the prototype (e.g. wind tunnel model of an aircraft, hydraulic model of a dam, etc.)

Dimensional analysis gives us the dimensional number

\( \Pi_1 = f(\Pi_2, \Pi_3, \ldots, \Pi_5) \)

.. exact same is valid for the model

\( \Pi_{1,m} = f(\Pi_{2,m}, \Pi_{3,m}, \ldots, \Pi_{5,m}) \)

To predict outcome on prototype based on model
we use the predictive equation:

\( \Pi_{1,m} = \Pi_1 \)

.. which is only valid if the so-called similarity conditions
(aka model design conditions or modeling laws) are met:

\( \Pi_{2,m} = \Pi_2, \) \(~~~~~\) \( \Pi_{3,m} = \Pi_3 \) \(~~~~~\) \( \ldots \) \(~~~~~\) \( \Pi_{5,m} = \Pi_5 \)

Types of Similarity

Three types of similarity:

    1. Geometric similarity: All geometric parameters are scaled equally
      2. \( \dfrac{L_m}{L_p} = \dfrac{D_m}{D_p} = \dfrac{H_m}{H_p} = \ldots = \text{constant} \)

    2. Kinematic similarity: Flow fields are scaled equally
      3. \( \dfrac{V_m}{V_p} = \dfrac{a_m}{a_p} = \ldots = \text{constant} \)

    3. Dynamic similarity: Forces are scaled equally
      4. \( \dfrac{F_{m,1}}{F_{p,1}} = \dfrac{F_{m,2}}{F_{p,2}} = \ldots = \text{constant} \)

Complete similarity if all three are fulfilled

Distorted models

When similarity conditions are not met, e.g.:

\( \Pi_{m,2} \neq \Pi_{p,2} \) \(~~\) or \(~~\) \( \Pi_{m,3} \neq \Pi_{p,3} \) \(~~\) \( \ldots \) \(~~\) or \(~~\) \( \Pi_{m,5} \neq \Pi_{p,5} \)

Then, the predictive equation is not valid

\( \Pi_{m,1} \neq \Pi_{p,1} \)

  • No general rule for when distorted models are accurate (requires experience)

Class exercise 5: Small ships in large oceans

Show that we can't use water test both model and prototype if we want to achieve complete similarity. Assume the dimensional groups have already been found to be the Reynolds and Froude numbers:

\( \text{Re} = \dfrac{V l}{\nu}, \) \(~~~~~\) \( \text{Fr} = \dfrac{V}{\sqrt{g L}}, \)