Fluid Mechanics

Analytical solutions for simple fluid flows

Lecturer: Jakob Hærvig

Slides by Jakob Hærvig (AAU Energy) and Jacob Andersen (AAU Build)

Complexities involved in Navier-Stokes equations

No universal analytical solution due to non-linearities ($u\partial u/\partial x$)

Solution approximated using numerical methods (e.g. CFD)
Solution found by experiments

Analytical solutions for only a few problems

Simple geometries: Flow between two plates or in a tube
Simple flows: Steady, laminar and fully-developed flows

x-direction: $$ \rho \left( \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z} \right) = -\frac{\partial p}{\partial x} + \mu \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \right) + \rho g_x $$ y-direction: $$ \rho \left( \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z} \right) = -\frac{\partial p}{\partial y} + \mu \left( \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} + \frac{\partial^2 v}{\partial z^2} \right) + \rho g_y $$ z-direction: $$ \rho \left( \frac{\partial w}{\partial t} + u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z} \right) = -\frac{\partial p}{\partial z} + \mu \left( \frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2} \right) + \rho g_z $$

Why look at these simplified problems?

Current research uses Poiseuille flow for verification of CFD

CO$_2$ diffuses into the fiber and is captured

Really (!) long fibres ($ l/D\approx12000$)
Steady, laminar, fully-developed flow is a very good assumption
Prescribed boundary condition

Results: Code verification results

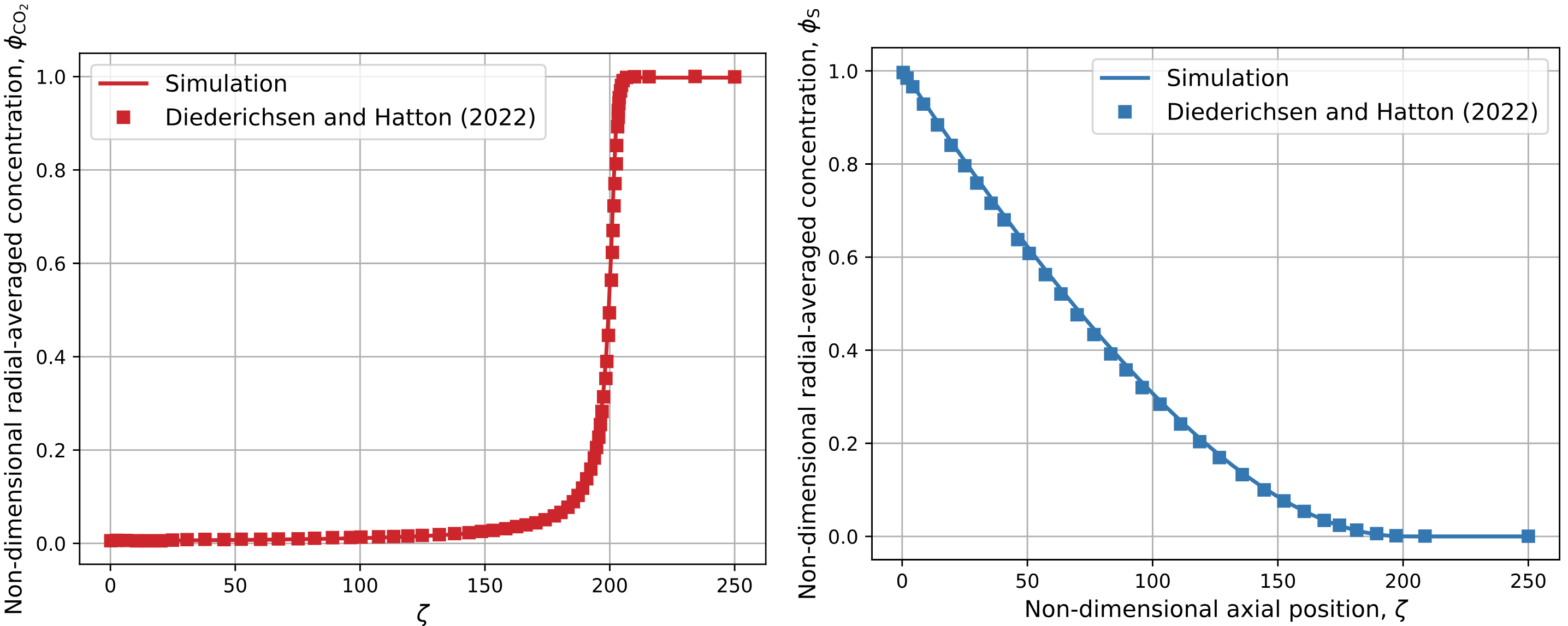
Figure: Hollow fibre membrane

Bazhenov, S. D., Bildyukevich, A. V., & Volkov, A. V. (2018). Gas-Liquid Hollow Fiber Membrane Contactors for Different Applications. Fibers, 6(4), 76. https://doi.org/10.3390/fib6040076

Code: Inlet boundary condition in OpenFOAM


/*--------------------------------*- C++ -*----------------------------------*\
  =========                 |
  \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox
   \\    /   O peration     | Website:  https://openfoam.com
    \\  /    A nd           | Version:  2506
     \\/     M anipulation  |
\*---------------------------------------------------------------------------*/
FoamFile
{
    format      ascii;
    class       volVectorField;
    location    "0";
    object      U;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

dimensions      [0 1 -1 0 0 0 0];

internalField   uniform (0 0 0);

boundaryField
{
    inlet
    {
        type    codedFixedValue;
        value   $internalField;  // dummy, gets overwritten by code

        name    parabolicInlet;

        code
        #{
            const scalar Uavg = 3.84e-05;  // Max velocity
            const vectorField& faceCentres = patch().Cf(); 
            static bool firstTime = true;
            static scalar R = -GREAT;

            vectorField& field = *this;

            if (firstTime)
            {  
                const pointField& points = patch().patch().points();

                forAll(points, i)
                {
                    R = max(R, points[i].x());
                }
                firstTime = false;
            }

            forAll(field, i)
            {
                scalar x = faceCentres[i].x();
                scalar z = faceCentres[i].z();
                scalar r = sqrt(x*x + z*z);
                scalar Uy = 2*Uavg * (1.0 - r*r/R/R);
                field[i] = vector(0, Uy, 0);
            }
        #};
    }
    upper_inner
    {
        type            zeroGradient;
        value           $internalField;
    }
    farfield
    {
        type            fixedValue;
        value           uniform (0 0 0);
    }
    "wedge.*"
    {
        type            wedge;
    }
}


// ************************************************************************* //

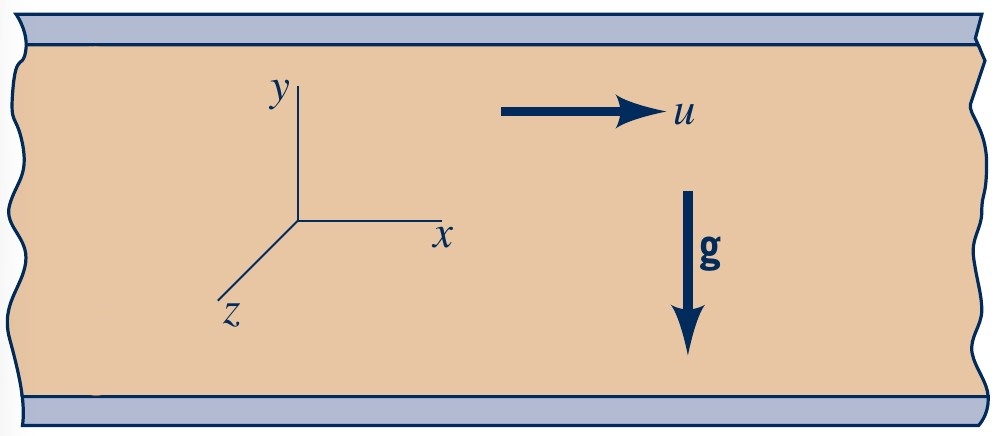
Flow between plates

Incompressible, steady, fully developed, laminar flow between two infinite plates

Velocity only in $x$-direction:
- then, $u=u(y)$, $v=w=0$
Steady flow:
- then, $\partial u/\partial t = \partial v/\partial t = \partial w/\partial t = 0$
By continuity equation: $\partial u/\partial x + \partial v/\partial y + \partial w/\partial z = 0$
- then, $\partial u/\partial x=0$
No gravity in $x$ and $z$ directions:
- then, $g_x = g_z = 0$

Navier-Stokes equations reduce to:

$x:~$$ 0 = -\dfrac{\partial p}{\partial x} + \mu \dfrac{\partial^2 u}{\partial y^2}$,$~~~y:~$$ 0 = -\dfrac{\partial p}{\partial y} + \rho g_y $,$~~~z:~$$ 0 = -\dfrac{\partial p}{\partial z}$

$x$-direction:

$ \rho $ $ \bigg( $ $ \dfrac{\partial u}{\partial t} $ $ + $ $ u \dfrac{\partial u}{\partial x} $ $ + $ $ v \dfrac{\partial u}{\partial y} $ $ + $ $ w \dfrac{\partial u}{\partial z} $ $ \bigg) = -$ $ \dfrac{\partial p}{\partial x} $ $ + $ $ \mu $ $ \bigg( $ $ \dfrac{\partial^2 u}{\partial x^2} $ $ + $ $ \dfrac{\partial^2 u}{\partial y^2} $ $ + $ $ \dfrac{\partial^2 u}{\partial z^2} $ $ \bigg) + $ $ \rho g_x $

$y$-direction:

$ \rho $ $ \bigg( $ $ \dfrac{\partial v}{\partial t} $ $ + $ $ u \dfrac{\partial v}{\partial x} $ $ + $ $ v \dfrac{\partial v}{\partial y} $ $ + $ $ w \dfrac{\partial v}{\partial z} $ $ \bigg) = -$ $ \dfrac{\partial p}{\partial y} $ $ + $ $ \mu $ $ \bigg( $ $ \dfrac{\partial^2 v}{\partial x^2} $ $ + $ $ \dfrac{\partial^2 v}{\partial y^2} $ $ + $ $ \dfrac{\partial^2 v}{\partial z^2} $ $ \bigg) + $ $ \rho g_y $

$z$-direction:

$ \rho $ $ \bigg( $ $ \dfrac{\partial w}{\partial t} $ $ + $ $ u \dfrac{\partial w}{\partial x} $ $ + $ $ v \dfrac{\partial w}{\partial y} $ $ + $ $ w \dfrac{\partial w}{\partial z} $ $ \bigg) = -$ $ \dfrac{\partial p}{\partial z} $ $ + $ $ \mu $ $ \bigg( $ $ \dfrac{\partial^2 w}{\partial x^2} $ $ + $ $ \dfrac{\partial^2 w}{\partial y^2} $ $ + $ $ \dfrac{\partial^2 w}{\partial z^2} $ $ \bigg) + $ $ \rho g_z $

Flow between two stationary plates

Integrating twice to get $ u(y)$:

$ \dfrac{\partial^2 u}{\partial y^2} = \dfrac{1}{\mu} \dfrac{\partial p}{\partial x} $

$\dfrac{\partial u}{\partial y} = \dfrac{1}{\mu} \dfrac{\partial p}{\partial x} y + C_1 $

$ u = \dfrac{1}{2\mu} \dfrac{\partial p}{\partial x} y^2 + C_1 y + C_2 $

Using boundary conditions:

At $y=\pm h~$ we have $ u = 0$

$ C_1 = 0 $, $ C_2 = -\dfrac{1}{2\mu} \dfrac{\partial p}{\partial x} h^2 $

Velocity profile (by inserting $C_1$ and $C_2$):

$ u(y) = \dfrac{1}{2\mu} \dfrac{\partial p}{\partial x} (y^2 - h^2) $

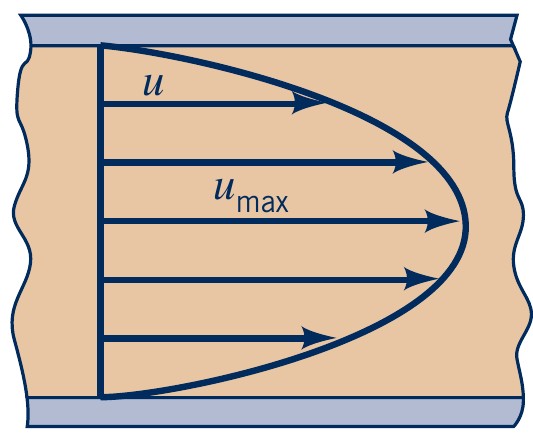
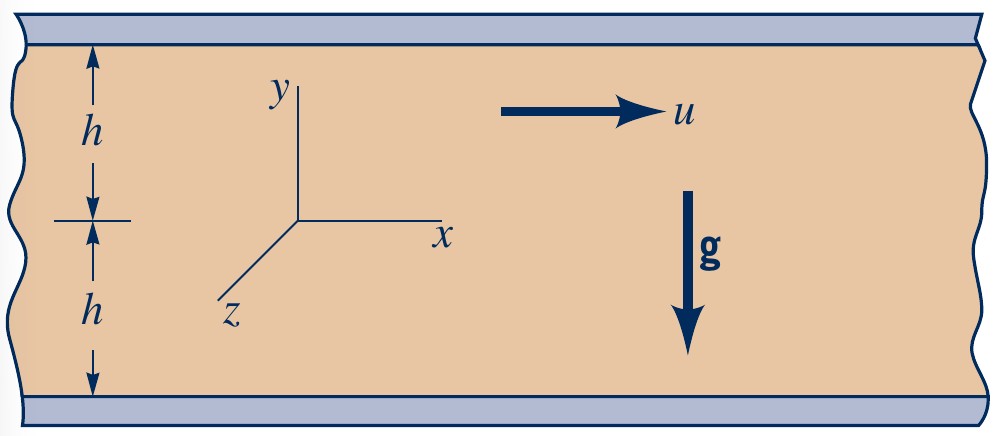
Volume flow rate (integrating velocity profile):

$ q = \int^h_{-h} u(y) = -\dfrac{2 h^3}{3\mu} \left(\dfrac{\partial p}{\partial x}\right) $

Average velocity:

$ V = \dfrac{q}{2h} = -\dfrac{h^2}{3\mu} \left(\dfrac{\partial p}{\partial x}\right) $

Maximum velocity (centre of channel, $y=0$):

$ u_{max} = u(y=0)=-\dfrac{h^2}{2\mu} \left(\dfrac{\partial p}{\partial x}\right) = \dfrac{3}{2} V $

Flow between one stationary and one moving plate (aka Couette flow)

Integrating twice to get $ u(y)$:

$ \dfrac{\partial^2 u}{\partial y^2} = \dfrac{1}{\mu} \dfrac{\partial p}{\partial x} $

$\dfrac{\partial u}{\partial y} = \dfrac{1}{\mu} \dfrac{\partial p}{\partial x} y + C_1 $

$ u = \dfrac{1}{2\mu} \dfrac{\partial p}{\partial x} y^2 + C_1 y + C_2 $

Using boundary conditions:

At $y=0~$ we have $ u = 0$

At $y=b~$ we have $ u = U$

Finding $C_1$ and $C_2$ and inserting:

$ u(y) = U \dfrac{y}{b} + \dfrac{1}{2\mu} \dfrac{\partial p}{\partial x} (y^2 - by) $

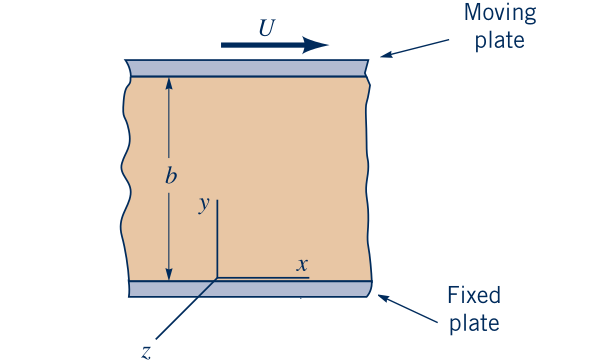
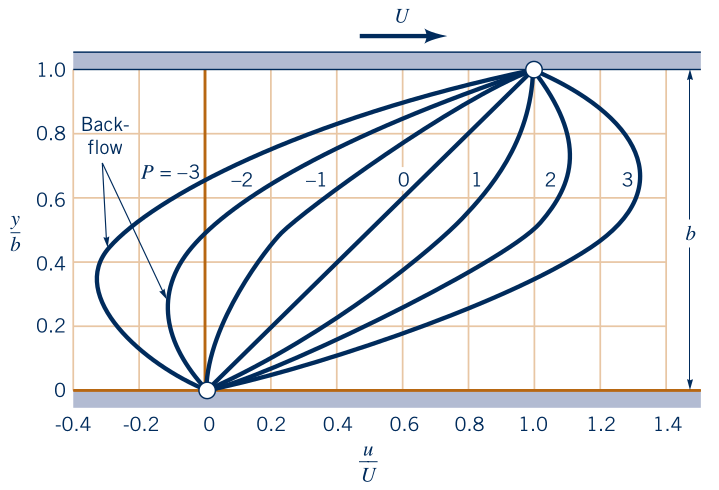
$ P = -\dfrac{b^2}{2\mu U} \left( \dfrac{\partial p}{\partial x} \right) $

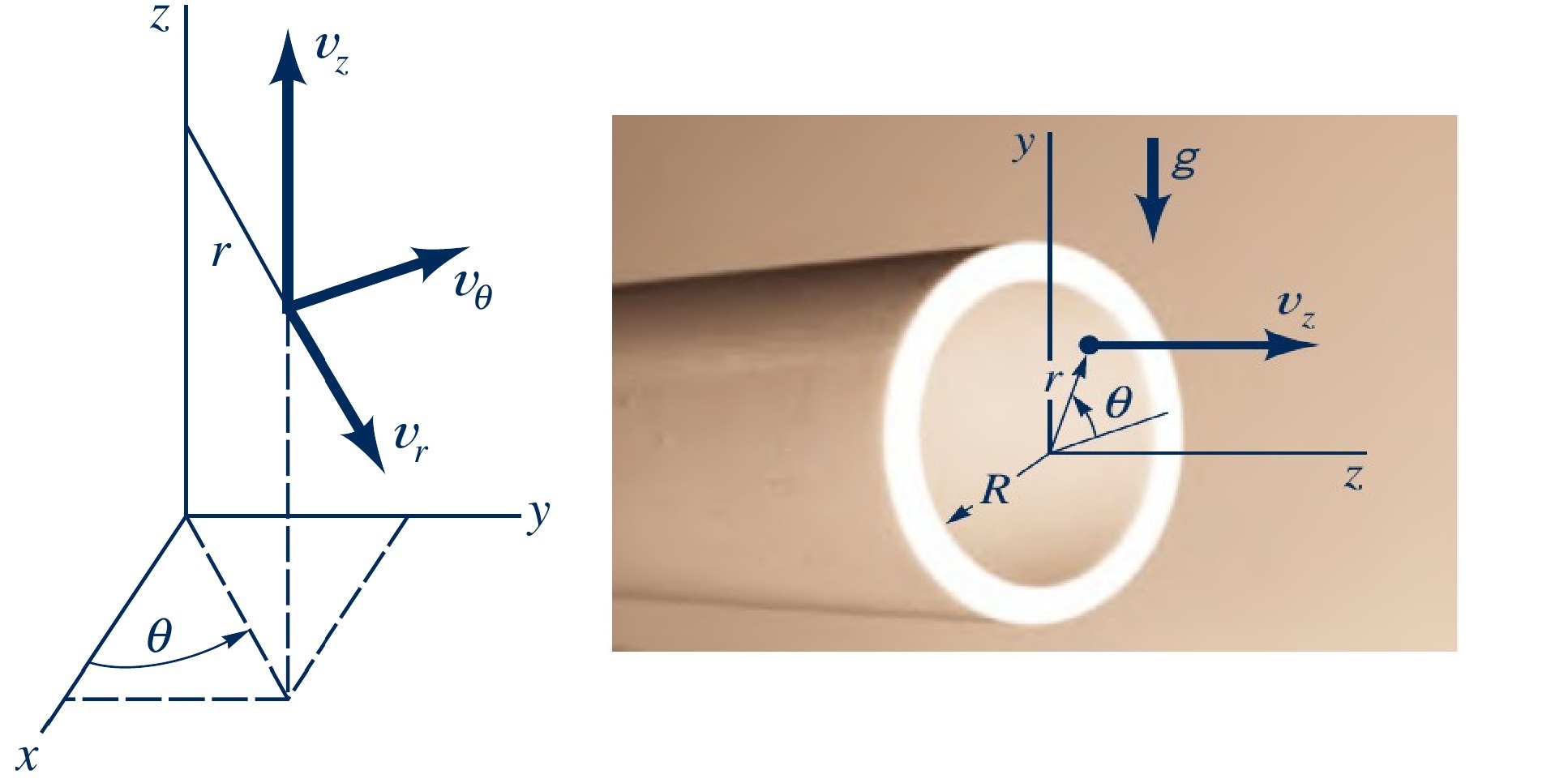
Flow in a circular pipe (aka Poiseuille flow)

Incompressible, steady, fully developed, laminar flow in a circular pipe

Velocity only in $z$-direction:
- then, $v_z = v_z(r)$, $v_\theta=v_r=0$
Steady flow:
- then, $\partial u/\partial t = \partial v/\partial t = \partial w/\partial t = 0$
By continuity equation: $\dfrac{1}{r}\dfrac{\partial (r v_r)}{\partial r} + \dfrac{1}{r} \dfrac{\partial v_\theta}{\partial \theta} + \dfrac{\partial v_z}{\partial z} = 0$
- then, $\partial v_z/\partial z=0$
No gravity in $z$ direction:
- then, $g_z=0$

Navier-Stokes equations reduce to:

$z:~$$ 0 = -\dfrac{\partial p}{\partial z} + \mu \dfrac{1}{r}\dfrac{\partial}{\partial r} \left(r \dfrac{\partial v_z}{\partial r} \right)$,$~~~r:~$$ 0 = \rho g_r - \dfrac{\partial p}{\partial r} $,$~~~\theta:~$$ 0 = \rho g_\theta -\dfrac{1}{r}\dfrac{\partial p}{\partial \theta}$

Integration, applying boundary condtions and find $C_1$ and $C_2$:

$ v_z(r) = \dfrac{1}{4\mu}-\left(\dfrac{\partial p}{\partial z}\right)\left(r^2-R^2\right)$

Velocity is a function of viscosity $\mu$, pressure gradient $\partial p/ \partial z$ and pipe radius $R$.

$z$-direction:

$ \rho $ $ \bigg( $ $ \dfrac{\partial v_z}{\partial t} $ $ + $ $ v_r \dfrac{\partial v_z}{\partial r} $ $ + $ $ \dfrac{v_\theta}{r} \dfrac{\partial v_z}{\partial \theta} $ $ + $ $ v_z \dfrac{\partial v_z}{\partial z} $ $ \bigg) = -$ $ \dfrac{\partial p}{\partial z} $ $ + $ $ \mu $ $ \bigg( $ $ \dfrac{1}{r}\dfrac{\partial }{\partial r} \bigg( r \dfrac{\partial v_z}{\partial r} \bigg) $ $ + $ $ \dfrac{1}{r^2}\dfrac{\partial^2 v_z}{\partial \theta^2} $ $ + $ $ \dfrac{\partial^2 v_z}{\partial z^2} $ $ \bigg) + $ $ \rho g_z $

$r$-direction:

$ \rho $ $ \bigg( $ $ \dfrac{\partial v_r}{\partial t} $ $ + $ $ v_r \dfrac{\partial v_r}{\partial r} $ $ + $ $ \dfrac{v_\theta}{r} \dfrac{\partial v_r}{\partial \theta} $ $ - $ $ \dfrac{v_\theta^2}{r} $ $ + $ $ v_z \dfrac{\partial v_r}{\partial z} $ $ \bigg) = -$ $ \dfrac{\partial p}{\partial r} $ $ + $ $ \mu $ $ \bigg( $ $ \dfrac{1}{r}\dfrac{\partial }{\partial r} \bigg( r \dfrac{\partial v_r}{\partial r} \bigg) $ $ - $ $ \dfrac{v_r}{r^2} $ $ + $ $ \dfrac{1}{r^2}\dfrac{\partial^2 v_r}{\partial \theta^2} $ $ - $ $ \dfrac{2}{r^2}\dfrac{\partial v_r}{\partial \theta} $ $ + $ $ \dfrac{\partial^2 v_r}{\partial z^2} $ $ \bigg) + $ $ \rho g_r $

$\theta$-direction:

$ \rho $ $ \bigg( $ $ \dfrac{\partial v_\theta}{\partial t} $ $ + $ $ v_r \dfrac{\partial v_\theta}{\partial r} $ $ + $ $ \dfrac{v_\theta}{r} \dfrac{\partial v_\theta}{\partial \theta} $ $ - $ $ \dfrac{v_r v_\theta}{r} $ $ + $ $ v_z \dfrac{\partial v_\theta}{\partial z} $ $ \bigg) = -$ $ \dfrac{1}{r}\dfrac{\partial p}{\partial \theta} $ $ + $ $ \mu $ $ \bigg( $ $ \dfrac{1}{r}\dfrac{\partial }{\partial r} \bigg( r \dfrac{\partial v_\theta}{\partial r} \bigg) $ $ - $ $ \dfrac{v_\theta}{r^2} $ $ + $ $ \dfrac{1}{r^2}\dfrac{\partial^2 v_\theta}{\partial \theta^2} $ $ + $ $ \dfrac{2}{r^2}\dfrac{\partial v_r}{\partial \theta} $ $ + $ $ \dfrac{\partial^2 v_\theta}{\partial z^2} $ $ \bigg) + $ $ \rho g_\theta $

Details on flow in circular pipes (aka Poiseuille flow)

Volume flow rate (integrate velocity):

$$ Q = 2\pi \int_0^R v_z(r) r dr = -\dfrac{\pi R^4}{8\mu} \left(\dfrac{\partial p}{\partial z}\right) = \dfrac{\pi R^4 \Delta p}{8\mu l}$$

Flow rate is a function of viscosity $\mu$, pressure gradient $\partial p/ \partial z$ and pipe radius $R$.

Average velocity (divide by area):

$$ V = \dfrac{Q}{A} = \dfrac{-\dfrac{\pi R^4}{8\mu} \left(\dfrac{\partial p}{\partial z}\right)}{\pi R^2} = -\dfrac{R^2}{8\mu} \left(\dfrac{\partial p}{\partial z}\right) = \dfrac{R^2 \Delta p}{8\mu l}$$

Mean velocity is a function of viscosity $\mu$, pressure gradient $\partial p/ \partial z$ and pipe radius $R$.

Maximum velocity ($r=0$):

$$ v_z(r=0) = \dfrac{1}{4\mu}-\left(\dfrac{\partial p}{\partial z}\right)(0^2-R^2)=-\dfrac{R^2}{4\mu} \left(\dfrac{\partial p}{\partial z}\right) = \dfrac{R^2 \Delta p}{4\mu l}$$

Mean velocity is a function of viscosity $\mu$, pressure gradient $\partial p/ \partial z$ and pipe radius $R$.

Ratio of centerline to mean velocity ($v_z(r=0)/V$):

$$ \dfrac{v_z(r=0)}{V} = \dfrac{\dfrac{R^2 \Delta p}{4\mu l}}{\dfrac{R^2 \Delta p}{8\mu l}} = 2$$

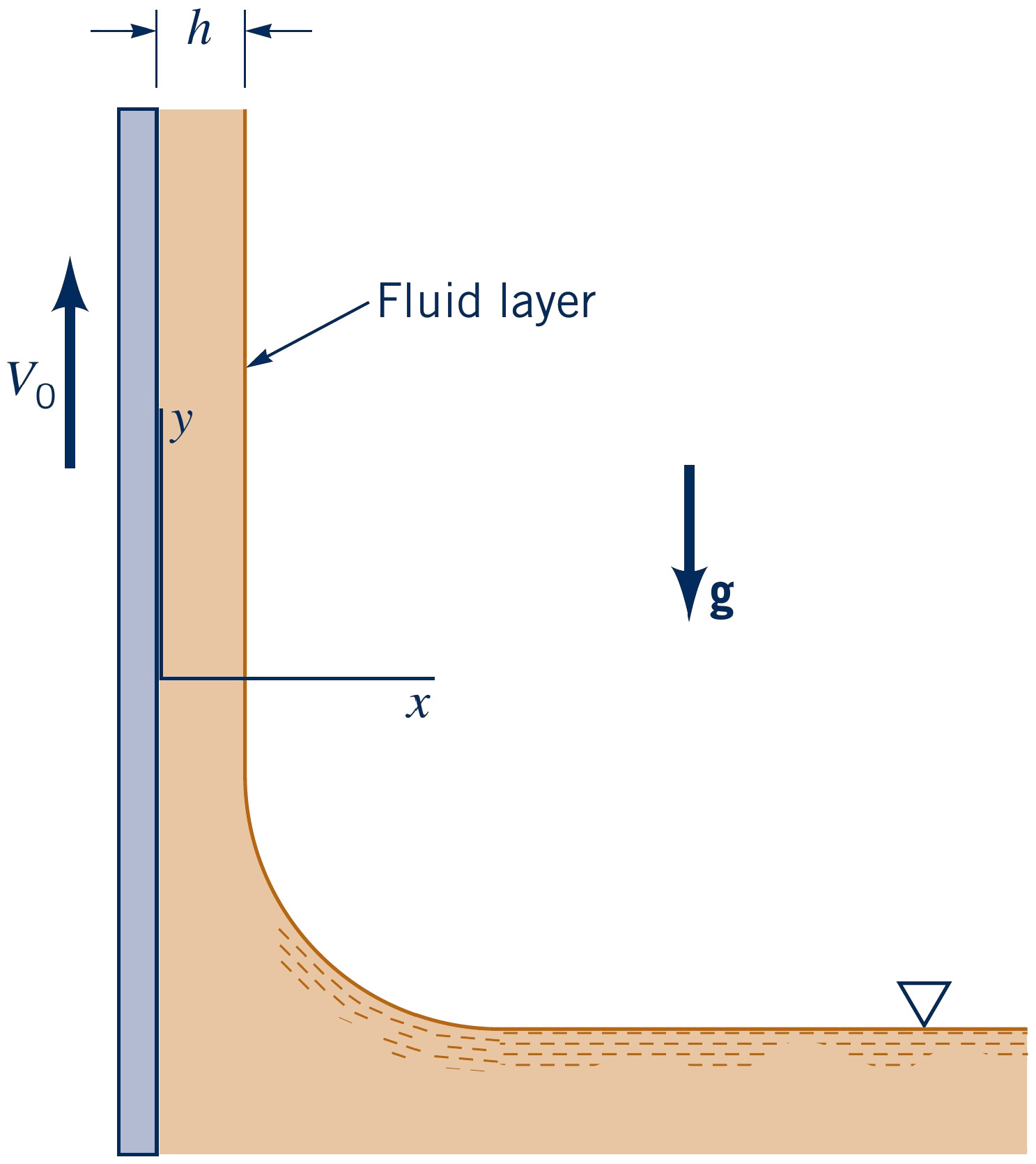
Centerline velocity is exactly twice the mean velocity.

Exercise: Upward moving fluid film

A wide moving belt passes through a container of a viscous liquid. The belt moves vertically upward with a constant velocity, $V_0$, as illustrated in the figure. Because of viscous forces the belt picks up a film of fluid of thickness $h$. Gravity tends to make the fluid drain down the belt. Assume that the flow is laminar, steady, and fully developed.

$$ \rho \left( \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z} \right) = -\frac{\partial p}{\partial x} + \mu \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \right) + \rho g_x $$ $$ \rho \left( \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z} \right) = -\frac{\partial p}{\partial y} + \mu \left( \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} + \frac{\partial^2 v}{\partial z^2} \right) + \rho g_y $$ $$ \rho \left( \frac{\partial w}{\partial t} + u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z} \right) = -\frac{\partial p}{\partial z} + \mu \left( \frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2} \right) + \rho g_z $$